6.1.3 VGGNet
등장 배경 : 합성곱층의 파라미터 개수를 줄이고, 훈련 시간 개선을 위해
VGG16 네트워크의 구조적 세부 사항

* 모든 합성곱 커널의 크기 : 3×3
* 모든 최대 풀링 커널 크기 : 2×2
+ 스트라이드 : 2
VGGNet16 구조 상세
| 층 유형 | 특성 맵 | 크기 | 커널 크기 | 스트라이드 | 활성화 함수 |
| 이미지 | 1 | 224×224 | – | – | – |
| 합성곱층 | 64 | 224×224 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 64 | 224×224 | 3×3 | 1 | 렐루(ReLU) |
| 최대 풀링층 | 64 | 112×112 | 2×2 | 2 | – |
| 합성곱층 | 128 | 112×112 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 128 | 112×112 | 3×3 | 1 | 렐루(ReLU) |
| 최대 풀링층 | 128 | 56×56 | 2×2 | 2 | – |
| 합성곱층 | 256 | 56×56 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 256 | 56×56 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 256 | 56×56 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 256 | 56×56 | 3×3 | 1 | 렐루(ReLU) |
| 최대 풀링층 | 256 | 28×28 | 2×2 | 2 | – |
| 합성곱층 | 512 | 28×28 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 512 | 28×28 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 512 | 28×28 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 512 | 28×28 | 3×3 | 1 | 렐루(ReLU) |
| 최대 풀링층 | 512 | 14×14 | 2×2 | 2 | – |
| 합성곱층 | 512 | 14×14 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 512 | 14×14 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 512 | 14×14 | 3×3 | 1 | 렐루(ReLU) |
| 합성곱층 | 512 | 14×14 | 3×3 | 1 | 렐루(ReLU) |
| 최대 풀링층 | 512 | 7×7 | 2×2 | 2 | – |
| 완전연결층 | – | 4096 | – | – | 렐루(ReLU) |
| 완전연결층 | – | 4096 | – | – | 렐루(ReLU) |
| 완전연결층 | – | 1000 | – | – | 소프트맥스(softmax) |
실습 - VGG19 모델 생성
1. 필요한 라이브러리 호출
import cv2 //얼굴 인식, 물체 식별, 이미지 결합 등 작업이 가능한 오픈 소스 라이브러리
2. VGG19 네트워크 생성
Model Subclassing API 이용
class VGG19(Sequential):
def __init__(self, input_shape):
super().__init__()
self.add(Conv2D(64, kernel_size=(3, 3), padding='same', activation='relu', input_shape=input_shape))
self.add(Conv2D(64, kernel_size=(3, 3), padding='same', activation='relu'))
self.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
self.add(Conv2D(128, kernel_size=(3, 3),padding='same', activation='relu'))
self.add(Conv2D(128, kernel_size=(3, 3), padding='same', activation='relu'))
self.add(MaxPooling2D(pool_size=(2, 2), strides= (2, 2)))
...
self.add(Flatten())
self.add(Dense(4096, activation='relu'))
self.add(Dropout(0.5))
self.add(Dense(4096, activation='relu'))
self.add(Dropout(0.5))
self.add(Dense(1000, activation='softmax'))
self.compile(optimizer=tf.keras.optimizers.Adam(0.003),
loss='categorical_crossentropy',
metrics=['accuracy'])
3. VGG19 모델 생성
2의 클래스를 호출하여 모델 생성
model = VGG19(input_shape=(224, 224, 3)) //VGG19클래스에 전달되는 입력값 형태
4. 사전 훈련된 VGG19 가중치 내려받기 & 클래스 정의
VGG19모델의 파라미터 : 1억 4000만 개 → 네트워크 훈련 시간이 오래걸림
→ 여기선 사전 훈련된 모델에서 가중치를 가져와 사용 by load_weights()
#사전 훈련된 VGG19 모델의 가중치 내려받기
model.load_weights("../chap6/data/vgg19_weights_tf_dim_ordering_tf_kernels.h5")
#검증용으로 사용될 클래스 세개만 적용
classes={282: 'cat',
664: 'notebook, notebook computer',
970: 'alp'}
5. 이미지 호출 및 예측
이미지를 모델에 적용한 후 정확한 분류로 예측이 되었는지 검증
image1 = plt.imread("../chap6/data/labtop.jpg")
#image1 = cv2.imread("../chap6/data/starrynight.jpeg")
#image1 = cv2.imread("../chap6/data/cat.jpg")
image1 = cv2.resize(image1, (224, 224))
plt.figure()
plt.imshow(image1)
image1 = image1[np.newaxis, :] #차원 확장(행을 추가)
predicted_value = model.predict_classes(image1) ---- ①
plt.title(classes[predicted_value[0]]) #출력에 대한 제목 지정
① predict() VS predict_classes
- predict() 반환값 : 숫자 값, 샘플이 각 범주에 속할 확률을 나타냄
- predict_classes() 반환 값 : 샘플이 속한 카테고리 레이블
예) predict()의 반환값은 [[0.23522541] [0.9731412]], predict_classes()의 반환값은 [[0] [1]] 형태
🚫오류
- error: (-215:Assertion failed) !ssize.empty() in function 'cv::resize'
- Image data of dtype object cannot be converted to float
⇒ cv2.imread -> plt.imread로 해결
+ 또 다른 이미지로 테스트를 진행하고 싶다면 https://unsplash.com/ 웹 사이트에서 이미지를 내려받아 진행
6.1.4 GoogLeNet
GoogLeNet이란?
주어진 하드웨어 자원을 최대한 효율적으로 이용, 학습 능력은 극대화함
인셉션 모듈의 추가
인셉션 모듈 : 특징을 효율적으로 추출하기 위해 1×1, 3×3, 5×5의 합성곱 연산을 각각 수행
//3×3 최대 풀링은 입력과 출력의 높이와 너비가 같아야하므로, 패딩 연산 추가 必(풀링 연산에선 드문 케이스)
⇒ 결과적으로 GoogLeNet에 적용된 해결 방법 : 희소 연결
//희소 연결 : CNN은 합성곱, 풀링, 완전연결층이 서로 밀집하게 연결되어 있는데,
빽빽하게 연결된 신경망 대신 '관련성'이 높은 노드끼리만 연결하는 방법(효과 : 연산량↓, 과적합 해결 가능)
GoogLeNet의 인셉션 모듈

인셉션 모듈의 네 가지 연산
• 1×1 합성곱
• 1×1 합성곱 + 3×3 합성곱
• 1×1 합성곱 + 5×5 합성곱
• 3×3 최대 풀링 + 1×1 합성곱
합성곱 신경망에서 자주 나타나는 문제
심층 신경망의 계층이 넓고(뉴런이 많고), 깊으면(계층이 많으면)
→ 장점 : 인식률은 좋아짐
→ 단점 : 과적합, 기울기 소멸 문제, 학습 시간 지연, 연산 속도 등의 문제 발생
⇒ GoogLeNet(인셉션)으로 해결 가능
6.1.5 ResNet
ResNet 핵심
깊어진 신경망을 효과적으로 학습하기 위한 방법으로 레지듀얼(residual; 잔여) 개념을 고안한 것
신경망 깊이가 깊어질 수록
- 딥러닝 성능은 좋아짐 (X)
- 성능이 좋아지다가 일정한 단계에 다다르면 성능이 나빠짐 (O)
네트워크 깊이에 따른 성능 비교

훈련 에러 / 검증 에러
네트워크 56층이 20층보다 더 나쁜 성능을 보임
⇒ 깊이가 깊다고 해서 무조건 성능이 좋아지는 것 X
→ ResNet : 문제 해결을 위해 레지듀얼 블록(residual block) 도입
레지듀얼 블록 : 기울기가 잘 전파될 수 있도록 일종의 숏컷(shortcut, skip connection; 비선형 처리 계층을 건너뛰고 신경 네트워크의 서로 다른 계층에 있는 노드 간의 추가 연결)을 만들어줌
- ResNet은 층이 총 152개(GoogLeNet은 22개) → 기울기 소멸 문제가 발생할 수 있으므로 숏컷을 두어 기울기 소멸 문제를 방지함
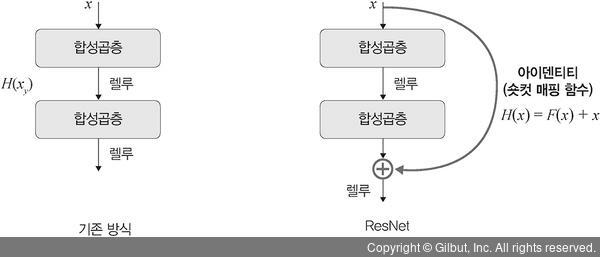
기존 신경망
목적 : 입력 값 x를 출력 값 y로 매핑하는 함수 H(x)를 얻는 것
ResNet
목적 : F(x)+x를 최소화하는 것
//F(x) : 레지듀얼 함수, 두 개의 합성곱층 사이에 위치
- 출력(H(x))과 입력 x에 대한 차(F(x)=H(x)-x)로 표현 가능
- x는 현시점에서 변할 수 없는 값 → F(x)를 0에 가깝게 만드는 것이 목적
- F(x)가 0이 되면 출력과 입력 모두 x로 같아지게 됨
- 즉, F(x)=H(x)-x이므로 F(x)를 최소로 한다는 것은 H(x)-x를 최소로 한다는 것과 의미가 동일
- H(x)-x를 레지듀얼이라 함
📈ResNet 기울기 소멸 문제 해결 과정 정리
1. 입력(x)과 레이블(y) 관계를 설명하는 함수 H(x) = x가 되도록 학습시킴
2. F(x)가 0이 되도록 학습시킴
3. F(x) + x = H(x) = x가 되도록 학습시키면, F(x)+x의 미분 값은 F′(x)+1로, 최소 1 이상의 값이 도출됨
4. 모든 계층에서 기울기가 F′(x)+1 ⇒ (오차가 0에 가깝게 수렴하여 발생하는) 기울기 소멸 문제가 해결됨
ResNet 구조
= 아이덴티티 블록(숏컷으로 만들어진 블록) + 합성곱 블록(합성곱층으로 구성됨)

아이덴티티 블록
네트워크의 매핑함수 F(x)에 입력 x를 그대로 더함

합성곱 블록
입력 x가 1×1 합성곱층을 거친 후 F(x)에 더해 줌

ResNet 구조
두 블록을 왼쪽 그림처럼 쌓아서 구성
🛠ResNet 구조
VGG19 구조를 뼈대 + 합성곱층을 추가해 깊게 만듦 + 숏컷 추가
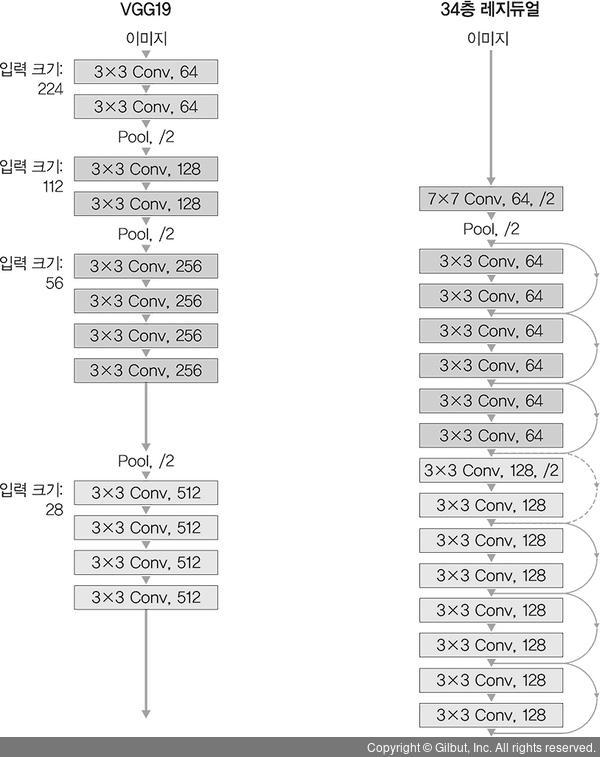
실습 - 아이덴티티 블록, 합성곱 블록
아이덴티티 블록
def res_identity(x, filters):
x_skip = x //입력값
f1, f2 = filters
x = Conv2D(f1, kernel_size=(1, 1), strides=(1, 1), padding='valid', kernel_regularizer=I2(0.001))(x) --- ①
x = BatchNormalization()(x) --- ②
x = Activation(activations.relu)(x) #첫번째 블록
x = Conv2D(f1, kernel_size=(3, 3), strides=(1, 1), padding='same', kernel_regularizer=I2(0.001))(x)
x = BatchNormalization()(x)
x = Activation(activations.relu)(x) #두번째 블록
x = Conv2D(f2, kernel_size=(1, 1), strides=(1, 1), padding='valid', kernel_regularizer=I2(0.001))(x)
x = BatchNormalization()(x) #세번째 블록
x = Add()([x, x_skip]) #숏컷
x = Activation(activations.relu)(x)
return x
① kernel_regularizier : Regularizer to apply a penalty on the layer's kernel(These penalties are summed into the loss function that the network optimizes)
② BatchNormalization : 데이터의 평균을 0으로, 표준편차를 1로 분포시킴
각 계층에서 입력 데이터의 분포는 앞 계층에서 업데이트된 가중치에 따라 변함.
→ 각 계층마다 변화되는 분포는 학습 속도를 늦춤 + 학습을 어렵게 함
합성곱 블록
def res_conv(x, s, filters): #입력, 스트라이드 크기, 필터 개수 배열
x_skip = x
f1, f2 = filters
x = Conv2D(f1, kernel_size=(1, 1), strides=(s, s), padding='valid', kernel_regularizer=l2(0.001))(x)
x = BatchNormalization()(x)
x = Activation(activations.relu)(x) #첫번째 블록
x = Conv2D(f1, kernel_size=(3, 3), strides=(1, 1), padding='same', kernel_regularizer=l2(0.001))(x)
x = BatchNormalization()(x)
x = Activation(activations.relu)(x) #두번째 블록
x = Conv2D(f2, kernel_size=(1, 1), strides=(1, 1), padding='valid', kernel_regularizer=l2(0.001))(x)
x = BatchNormalization()(x) #세번째 블록
x_skip = Conv2D(f2, kernel_size=(1, 1), strides=(s, s), padding='valid', kernel_regularizer=l2(0.001))(x_skip)
x_skip = BatchNormalization()(x_skip) #숏컷
x = Add()([x, x_skip])
x = Activation(activations.relu)(x)
return x
'Etc > Deep Learning' 카테고리의 다른 글
| 6장 합성곱 신경망Ⅱ(5) - 이미지 분할을 위한 신경망(U-Net부터 내용추가하기) (0) | 2021.08.17 |
|---|---|
| 6장 합성곱 신경망(4) - 객체 인식을 위한 신경망(R-CNN, 공간 피라미드 풀링, Fast R-CNN, Faster R-CNN) (0) | 2021.08.12 |
| 6장 합성곱 신경망Ⅱ(2) - 이미지 분류를 위한 신경망(AlexNet) (0) | 2021.08.10 |
| 6장 합성곱 신경망Ⅱ(1) - 이미지 분류를 위한 신경망(LeNet-5) + 실습 : 🔜파이썬 개념 추가 정리하기 (0) | 2021.08.09 |
| 5장 합성곱 신경망Ⅰ(4) - 그래프 합성곱 네트워크 (0) | 2021.08.09 |