5.1 합성곱 신경망
딥러닝의 역전파 : 복잡한 계산과정, 많은 자원을 요구
→ 해결방안 : 합성곱 신경망
(이미지 전체를 한 번에 계산X, 이미지의 국소적 부분을 계산 → 시간과 자원을 절약 ⇒ 이미지의 세밀한 부분까지 분석 가능)
5.1.1 합성곱층의 필요성
이미지 · 영상 처리에 유용
합성곱층의 원리
예) 3×3 흑백 이미지가 있다고 가정

이미지 분석 : 왼쪽 그림의 3×3 배열을 오른쪽 그림과 같이 펼침(flattening) → 각 픽셀에 가중치를 곱한 후 은닉층으로 전달
문제점 : 이미지를 펼쳐서 분석하면 데이터의 공간적 구조를 무시하게 됨
해결 방법 : 합성곱층
5.1.2 합성곱 신경망 구조
음성/이미지/영상 인식에서 주로 사용되는 신경망
다차원 배열 데이터를 처리하도록 구성됨(→ 컬러 이미지같은 다차원 배열 처리에 특화되어 있음)
합성곱 신경망의 다섯 개의 계층
- 입력층
- 합성곱층
- 풀링층
- 완전연결층
- 출력층

합성곱층, 풀링층을 거치면서 입력 이미지의 주요 특성 벡터를 추출
→ 그 후 추출된 주요 특성 벡터들은 완전 연결층을 거치며 1차원 벡터로 변환됨
→ 마지막으로 출력층에서 활성화 함수인 소프트맥스 함수를 사용, 최종 결과가 출력됨
1. 입력층
입력 이미지 데이터가 최초로 거치게 되는 계층
//이미지 : 단순 1차원 데이터X, 높이, 너비, 채널의 값을 갖는 3차원 데이터
//채널 : 이미지가 gray scale이면 1 값, 컬러(RGB)면 3 값을 가짐
예) 그림은 높이 4, 너비 4, 채널은 RGB를 가짐 ⇒ 이미지 형태는 (4, 4, 3)으로 표현

2. 합성곱층
입력 데이터에서 특성을 추출하는 역할
특성 추출 진행 과정
① 입력 이미지가 들어옴
② 이미지에 대한 특성을 감지하기 위해 커널이나 필터 사용, 커널/필터는 이미지의 모든 영역을 훑으면서 특성을 추출
③ 추출된 결과물 : 특성 맵(feature map)
// 이때 커널은 3×3, 5×5 크기로 적용되는 게 일반적, 스트라이드(stride) 간격에 따라 순차적으로 이동함
//스트라이드 : 필터를 적용하는 위치의 간격
그레이스케일 케이스>
스트라이드가 1일때 이동하는 과정
1단계. 입력 이미지에 3×3 필터 적용

입력 이미지와 필터를 포개놓고, 대응되는 숫자끼리 곱한 후 모두 더함
(1×1) + (0×0) + (0×1) + (0×0) + (1×1) + (0×0) + (0×1) + (0×0) + (1×1) = 3
2단계. 입력 이미지에 필터가 1만큼 이동

(0×1) + (0×0) + (0×1) + (1×0) + (0×1) + (0×0) + (0×1) + (1×0) + (1×1) = 1
3단계. 필터가 1만큼 두번째 이동

(0×1) + (0×0) + (0×1) + (0×0) + (0×1) + (1×0) + (1×1) + (1×0) + (0×1) = 1
4단계. 필터가 1만큼 '마지막'으로 이동
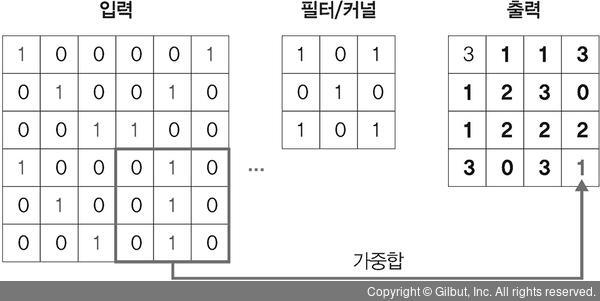
(0×1) + (1×0) + (0×1) + (0×0) + (1×1) + (0×0) + (0×1) + (1×0) + (0×1) = 1
결과 : (6, 6, 1) 이미지에 커널/스트라이드의 상호작용 ⇒ (4, 4, 1) 크기의 특성 맵으로 줄어듦
컬러 이미지의 합성곱>
gray scale과의 구분점
1. 필터 채널이 3
2. RGB 각각에 서로 다른 가중치로 합성곱을 적용한 후 결과를 더해줌
(스트라이드 및 연산하는 방법은 동일, ※필터 채널은 3이지만 필터 개수는 한 개)

필터가 두 개 이상인 합성곱>
필터가 두 개 이상이면, 필터 각각은 특성 추출 결과의 채널이 됨

합성곱층 요약
• 입력 데이터: W1×H1×D1(가로×세로×채널 또는 깊이)
• 하이퍼파라미터
• 필터 개수: K
• 필터 크기: F
• 스트라이드: S
• 패딩: P
//합성곱 연산을 수행하기 전, 입력데이터 주변을 특정값으로 채워 늘리는 것. 주로 출력데이터의 공간적 크기를 조절하기 위해 사용
• 출력 데이터
• W2 = (W1-F+2P)/S+1
• H2 = (H1-F+2P)/S+1
• D2 = K
3. 풀링층
특성 맵의 차원을 다운 샘플링
다운 샘플링 효과 : 연산량 감소시키고, 주요한 특성 벡터를 추출해 효과적인 학습을 하게 함
✔ 다운 샘플링이란?

이미지를 축소하는 것
풀링 연산
- 최대 풀링 : 대상 영역에서 최댓값을 추출
- 평균 풀링 : 대상 영역에서 평균을 반환
✔ 대부분의 합성곱 신경망에선 '최대 풀링'사용
//평균 풀링은 각 커널 값을 평균화시켜 중요한 가중치를 갖는 값의 특성이 희미해질 수 있음
최대 풀링의 연산 과정
첫번째 최대 풀링 과정
3, -1, -3, 1 값 중에서 최댓값(3)을 선택함

두번째 최대 풀링 과정
12, -1, 0, 1 값 중에서 최댓값(12)을 선택함

세번째 최대 풀링 과정
2, -3, 3, -2 값 중에서 최댓값(3)을 선택함

네번째 최대 풀링 과정

평균 풀링 계산 과정
'각 필터의 평균'으로 계산함
0 = (3+(-1)+(-3)+1)/4
3 = (12+(-1)+0+1)/4
0 = (2+(-3)+3+(-2))/4
1 = (0+1+4+(-1))/4
최대 풀링과 평균 풀링 결과 비교

최대 풀링, 평균 풀링 요약
• 입력 데이터: W1×H1×D1
• 하이퍼파라미터
• 필터 크기: F
• 스트라이드: S
• 출력 데이터
• W2 = (W1-F)/S+1
• H2 = (H1-F)/S+1
• D2 = D1
4. 완전연결층
합성곱층, 풀링층을 거쳐 차원이 축소된 특성맵을 전달받음
이미지를 3차원 벡터에서 1차원 벡터로 펼침(flatten)

5. 출력층
소프트맥스 활성화 함수를 사용해, 이미지가 각 레이블에 속할 확률 값을 출력(입력받은 값을 0~1 사이의 값으로 출력)
이때 가장 높은 확률 값을 갖는 레이블이 최종 값으로 선정됨
5.1.3 1D, 2D, 3D 합성곱
합성곱은 '이동하는 방향의 수'와 '출력 형태'에 따라 1D, 2D, 3D로 분류 가능
1. 1D 합성곱
필터가 시간을 축으로 좌우로만 이동할 수 있는 합성곱
→ 입력(W)과 필터(k)에 대한 출력은 W가 됨
✔ 그래프 곡선을 완화할 때 많이 사용
출력 형태 : 1D(dimension)의 배열
예) 입력이 [1, 1, 1, 1, 1]이고 필터가 [0.25, 0.5, 0.25] → 출력 : [1, 1, 1, 1, 1]

2. 2D 합성곱
필터가 방향 두 개로 움직이는 형태
입력(W, H)과 필터(k, k)에 대한 출력은 (W, H)가 됨
출력 형태 : 2D 행렬

3. 3D 합성곱
필터가 움직이는 방향이 세 개
입력(W, H, L)에 대해 필터(k, k, d)를 적용 → 출력으로 (W, H, L)을 갖는 형태
출력 형태 : 3D 형태(이때 d(깊이 필터) < L(길이 입력) 유지가 중요)

4. 3D 입력을 갖는 2D 합성곱
입력이 3D형태인데 출력은 2D 행렬을 취하는 합성곱
입력(W, H, L)에 필터(k, k, L)를 적용 → 출력은 (W, H)가 됨
//필터에 대한 길이(L)가 입력 채널의 길이(L)와 같아야하기 때문에 이런 합성곱 형태가 만들어짐. 즉 필터 L 길이 = 입력 L 길이
필터 : 두 방향으로 움직임
출력 형태 : 2D 행렬

5. 1×1 합성곱
입력(W, H, L)에 필터(1, 1, L)를 적용 → 출력은 (W, H)
채널(L) 개수를 조정해서 연산량이 감소되는 효과 有


합성곱층 패딩 참고 : https://excelsior-cjh.tistory.com/79
1X1 합성곱 이미지 출처 :https://velog.io/@dldydldy75/CNN-1x1-Convolution-%EA%B3%BC-%EC%BB%B4%ED%93%A8%ED%84%B0-%EB%B9%84%EC%A0%84
'Etc > Deep Learning' 카테고리의 다른 글
| 5장 합성곱 신경망Ⅰ(2) 실습- 전이학습- 특성 추출 기법(+ 텐서플로 허브) (0) | 2021.08.04 |
|---|---|
| 5장 합성곱 신경망Ⅰ(2) - 전이 학습 (0) | 2021.08.04 |
| 4장 딥러닝(2) - 딥러닝 알고리즘(심층 신경망, 합성곱 신경망, 순환 신경망, 제한된 볼츠만 머신, 심층 신뢰 신경망) (0) | 2021.08.04 |
| 4장 딥러닝(1) - 딥러닝 출현(퍼셉트론), 구조, 용어(수정, 보완必) (0) | 2021.08.04 |
| 4장 딥러닝 - 딥러닝 학습 | 딥러닝의 문제점, 해결 방안 | 딥러닝 이점 + α 옵티마이저 (0) | 2021.07.30 |