4.2.2 딥러닝 학습
딥러닝 학습 = 순전파 단계 → 역전파 단계

딥러닝 1단계. 순전파(feedforward)
- 네트워크에 훈련 데이터가 들어올 때 발생
- 데이터를 기반으로 예측 값을 계산하기 위해 전체 신경망을 교차해 지나감
= 모든 뉴런이 이전 층의 뉴런에서 수신한 정보에 변환(가중합 및 활성화 함수)을 적용, 다음층(은닉층)의 뉴런으로 전송하는 방식. 네트워크를 통해 입력 데이터를 전달, 데이터가 모든 층을 통과하고 모든 뉴런이 계산 완료하면, 그 예측 값은 최종 층(출력층)에 도달
그 다음 손실 함수로 네트워크의 손실 값(예측 값과 실제 값 차이, 오류) 추정
이때, 손실 함수 비용은 0이 이상적 (손실 함수 비용이 0에 가깝도록 하기위해 모델이 훈련을 반복하면서 가중치를 조정)
→ 손실이 계산되면 그 정보는 역으로 전파됨(출력층 → 은닉층 → 입력층) : 딥러닝 2단계. 역전파(backpropagation)
✔ 출력층에서 시작된 손실비용은 은닉층의 모든 뉴런으로 전파됨 BUT 은닉층의 뉴런은 각 뉴런의 가중치(원래 출력에 기여한 상대적 기여도)에 따라 값이 달라짐
∴ 출력층 → 은닉층 → 입력층 순서로 모든 뉴런에 대해 진행해 계산된 각 뉴런 결과를 다시 순전파의 가중치 값으로 사용
//신경망이란? : 뉴런의 연결 구조, 가중치를 스스로 학습해서 그 값을 찾아낼 수 있음
//뉴런이란? : 데이터와 계산이 흐르는 노드. 하나 이상의 입력 신호를 수신함
4.2.3 딥러닝의 문제점과 해결방안
딥러닝의 핵심 : 활성화 함수가 적용된 여러 은닉층을 결합하여 비선형 영역을 표현

활성화 함수가 적용된 은닉층 개수 多
→ 데이터 분류 잘 됨
BUT 은닉층이 많을 수록 생기는 세가지 문제점
1. 과적합 문제 발생
훈련 데이터에 대해 과하게 학습하여 실제 데이터에 대한 오차가 증가
과적합 발생 원인 : 훈련 데이터를 과하게 학습함
- 훈련데이터를 과하게 학습 → 예측값과 실제값 차이인 오차는 감소, 검증 데이터에 대해선 오차 증가

과적합 해결 방법 : 드롭아웃(dropout)
신경망 모델이 과적합되는 걸 피하기 위한 방법. 학습 과정 중 임의로 일부 노드들을 학습에서 제외시킴

드롭아웃 구현 코드
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28,28)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dropout(0.2), ------드롭아웃 적용
tf.keras.layers.Dense(10, activation='softmax')
])
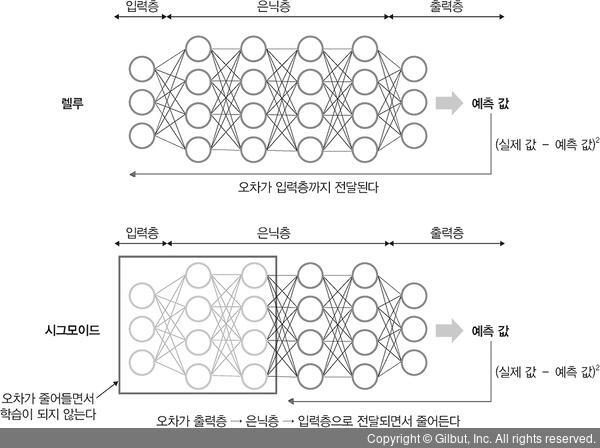
2. 기울기 소멸 문제 발생
은닉층이 많은 신경망에서 주로 발생, 출력층에서 은닉층으로 전달되는 오차가 크게 줄어들어 학습이 되지 않는 현상
= 기울기가 소멸 → 학습되는 양이 0에 가까워짐 → 학습이 더디게 진행됨 → 오차를 더 줄이지 못함 → 그 상태로 수렴
해결방법 : 시그모이드 · 하이퍼볼릭 탄젠트 대신 '렐루 활성화 함수'를 사용
3. 성능이 나빠지는 문제 발생
경사 하강법 : 손실 함수의 비용이 최소가 되는 지점을 찾을 때까지 기울기가 낮은 쪽으로 계속 이동하는 과정을 반복, 이때 성능이 나빠지는 문제가 발생함
문제 개선 방법 : 확률적 경사 하강법, 미니 배치 경사 하강법을 사용

경사 하강법이란?

배치 경사 하강법
- 전체 데이터셋에 대한 오류를 구한 후 기울기를 한 번만 계산하여 모델의 파라미터를 업데이트하는 방법
= 전체 훈련 데이터셋에 대해 가중치를 편미분하는 방법
- 단점 : 한 스텝에 모든 훈련 데이터셋을 사용 → 학습이 오래 걸림
⇒ 확률적 경사 하강법으로 단점을 개선
확률적 경사 하강법
- 임의로 선택한 데이터에 대해 기울기를 계산하는 방법
- 장점 : 빠른 계산이 가능(적은 데이터를 사용하므로)

파라미터 변경 폭이 불안정하고 때론 경사 하강법보다 정확도가 낮을 수 있지만 속도가 빠름
확률적 경사 하강법 구현 코드
model.fit(X_train, y_train, batch_size=1) ------ 임의로 선택한 데이터의 기울기를 계산하므로 batch_size=1이 됨
미니 배치(mini-batch) 경사 하강법
전체 데이터셋을 미니 배치(mini-batch) 여러 개로 나눔
→ 미니 배치 한 개마다 기울기를 구함
→ 그것의 평균 기울기를 이용해 모델을 업데이트해서 학습함

장점 : 전체 데이터를 계산하는 것보다 빠름, 확률적 경사 하강법보다 안정적 //실제로 가장 많이 이용함

확률적 경사 하강법에 비해 파라미터 변경 폭이 안정적이며 속도도 빠름
미니 매치 경사 하강법 구현 코드
model.fit(X_train, y_train, batch_size=32)
📝NOTE
옵티마이저
학습 속도와 운동량을 조정함
//확률적 경사 하강법의 파라미터 변경 폭이 불안정한 문제를 해결하기 위해 적용해 볼 수 있음
옵티마이저 유형

속도를 조정하는 방법
1. 아다그라드
변수(가중치)의 업데이트 횟수에 따라 학습률을 조정하는 방법
많이 변화한 변수는 최적 값에 근접했을 것이라는 가정하에 학습률을 작게하고, 적게 변화한 변수들은 학습률을 크게하여 빠르게 오차값을 줄이고자함
//파라미터마다 다른 학습률을 주기 위한 G함수. 이때 G값은 이전 G값의 누적(기울기 크기의 누적)
2. 아다델타
아다그라드에서 G값이 커짐에 따라 학습이 멈추는 문제를 해결하기 위한 방법
3. 알엠에스프롭
아다그라드의 G(i)값이 무한히 커지는 것을 방지하고자 제안된 방법
G값이 너무 크면 학습률이 작아져 학습이 안 될 수 있으므로, 사용자가 γ(감마)값을 이용하여 학습률 크기를 비율로 조정할 수 있게 함
운동량을 조정하는 방법
1. 모멘텀
경사 하강법과 동일하게 매번 기울기를 구하나, 가중치를 수정하기 전에 이전 수정방향(+, -)를 참조, 같은 방향으로 일정한 비율만 수정하는 방법
⇒ 수정이 양, 음의 방향으로 순차적으로 일어나는 지그재그 현상이 줄어듦, 이전 이동값을 고려하여 다음 값을 결정하므로 관성 효과를 얻을 수 있음
- '확률적 경사 하강법'과 함께 사용함
2. 네스테로프 모멘텀
기존 모멘텀 : 모멘턴 값 + 기울기 값 → 실제 값을 만듦
네스테로프 모멘텀 : 모멘텀 값이 적용된 지점에서 기울기 값을 계산 //관성 효과의 단점을 극복할 수 있음

속도와 운동량에 대한 혼용 방법
- 아담
모멘텀의 장점과 알엠에스프롭의 장점을 결합한 경사 하강법
4.2.4 딥러닝을 사용할 때 이점
1. 특성 추출
데이터별로 어떤 특징을 가지고 있는지 찾아내고, 그것을 토대로 데이터를 벡터로 변환하는 작업
(입력데이터를 분석하여 컴퓨터가 일정한 패턴이나 규칙을 찾아내기 위해선, 컴퓨터가 인지할 수 있는 데이터로 변환해야함)
딥러닝 활성화 이전엔 특성 추출이 매우 복잡했으나, 데이터 특징을 잘 잡아내고자 은닉층을 깊게 쌓는 방식으로 파라미터를 늘린 모델 구조를 사용하면서, 특징 추출 과정을 알고리즘에 통합시킴
2. 빅데이터의 효율적 활용
특성 추출을 알고리즘에 통합시킬 수 있었던 건 빅데이터 때문(딥러닝 학습을 이용한 특징 추출은 데이터 사례가 많을 수록 성능이 향상됨)
//확보된 데이터가 적다면 딥러닝의 성능 향상을 기대하기 어려우므로, 머신 러닝 고려해야함
'Etc > Deep Learning' 카테고리의 다른 글
| 4장 딥러닝(2) - 딥러닝 알고리즘(심층 신경망, 합성곱 신경망, 순환 신경망, 제한된 볼츠만 머신, 심층 신뢰 신경망) (0) | 2021.08.04 |
|---|---|
| 4장 딥러닝(1) - 딥러닝 출현(퍼셉트론), 구조, 용어(수정, 보완必) (0) | 2021.08.04 |
| 3장 머신러닝 - 비지도 학습(2) : 주성분 분석(PCA) (0) | 2021.07.27 |
| 3장(3) 실습 - 로지스틱 회귀 | 선형 회귀 (figure | enumerate | zip | subplot | np.reshape | digits | 혼동행렬 시각화 | train_test_split | y_pred) (0) | 2021.07.25 |
| 3장 머신러닝 - 비지도 학습(1) : K-평균 군집화, 밀도 기반 군집 분석 (0) | 2021.07.25 |