3.2 비지도 학습
비지도 학습이란?
레이블 필요X(지도학습은 필요), 정답이 없는 상태에서 훈련시키는 방법
K-평균 군집화를 사용하는 이유와 적용 환경
사용하는 이유 : 주어진 데이터에 대한 군집화
적용 환경 : 주어진 데이터셋을 이용하여 몇 개의 클러스터를 구성할 지 사전에 알 수 있을 때 사용하면 유용
비지도 학습의 군집과 차원 축소 비교
| 구분 | 군집 | 차원 축소 |
| 목표 | 데이터 그룹화 | 데이터 간소화 |
| 주요 알고리즘 | K-평균 군집화(K-Means) | 주성분 분석(PCA) |
| 예시 | 사용자의 관심사에 따라 그룹화하여 마케팅에 활용 |
- 데이터 압축 - 중요한 속성 도출 |
* 군집 = 군집화 = 클러스터(머신러닝)
3.2.1 K-평균 군집화
K-평균 군집화란?
데이터를 입력받아 소수의 그룹으로 묶는 알고리즘
레이블이 없는 데이터를 입력받아, 각 데이터에 레이블을 할당해서 군집화를 수행
K-평균 군집화 학습 과정
① 중심점 선택 : 랜덤하게 초기 중심점을 선택함(그림은 K=2로 초기화) //중심점과 클러스터는 K개
② 클러스터 할당 : K개의 중심점과 각각의 개별 데이터 간의 거리 측정, 가장 가까운 중심점을 기준으로 데이터를 할당
(이 과정에서 클러스터가 구성됨) //클러스터링 : 데이터를 하나 또는 둘 이상의 덩어리로 묶는 과정
③ 새로운 중심점 선택 : 클러스터마다 새로운 중심점을 계산
④ 범위 확인 : 선택된 중심점에 더 이상 변화X면 진행을 멈춤(계속 변화O면 1~3과정을 반복)

K-평균 군집화 알고리즘 사용을 권장하지 않는 경우(데이터 분류가 원하는 결과와 다르게 발생할 수 있음)
① 데이터가 비선형일 때

② 군집 크기가 다를 때

③ 군집마다 밀집도와 거리가 다를 때

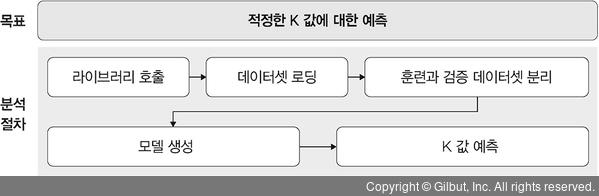
K-평균 군집화 예제 - 적정한 K값에 대한 예측
* K-평균 군집화 알고리즘의 성능은 K값에 따라 달라짐
+ 자료 유형
| 데이터 형태 | 설명 | 예시 |
| 수치형 자료 | 관측된 값이 수치로 측정됨 | 키, 몸무게, 시험 성적 |
| 연속형 자료 | 값이 연속적 | 키, 몸무게 |
| 이산형 자료 | 셀 수 있음 | 자동차 사고 |
| 범주형 자료 | 관측 결과가 몇 개의 범주 또는 항목의 형태로 나타남 | 성별(남, 여), 선호도(좋다, 싫다) |
| 순위형 자료 | 범주 간에 순서 의미가 있음 | '매우 좋다', '좋다', '그저 그렇다' 세 가지 범주가 주어졌을 때, 이 범주엔 순서가 있음 |
| 명목형 자료 | 범주 간에 순서 의미가 없음 | 혈액형 |
3.2.2 밀도 기반 군집 분석
밀도 기반 군집 분석이란?
일정 밀도 이상을 가진 데이터를 기준으로 군집을 형성하는 방법

밀도 기반 군집 분석을 사용하는 이유와 적용 환경
사용하는 이유 : 주어진 데이터에 대한 군집화
적용 환경 : 사전에 클러스터의 숫자를 알지 못할 때 사용하면 유용(≠ K-평균 군집화)
특징
- 노이즈에 영향 안 받음
- K-평균 군집화에 비해 연산량 많음
- 오목하거나 볼록한 부분을 처리하는데 유용(K-평균 군집화는 잘 처리 못함)

+ '노이즈'와 '이상치'의 차이
노이즈 : 주어진 데이터셋과 무관하거나, 무작위성 데이터로 전처리 과정에서 제거해야 할 부분(엡실론 범위 외 데이터)
이상치 : 관측된 데이터 범위에서 많이 벗어난 아주 작은 값이나 아주 큰 값

밀도 기반 군집 분석을 이용한 군집 방법 진행 절차
1단계. 엡실론 내 점 개수 확인 및 중심점 결정
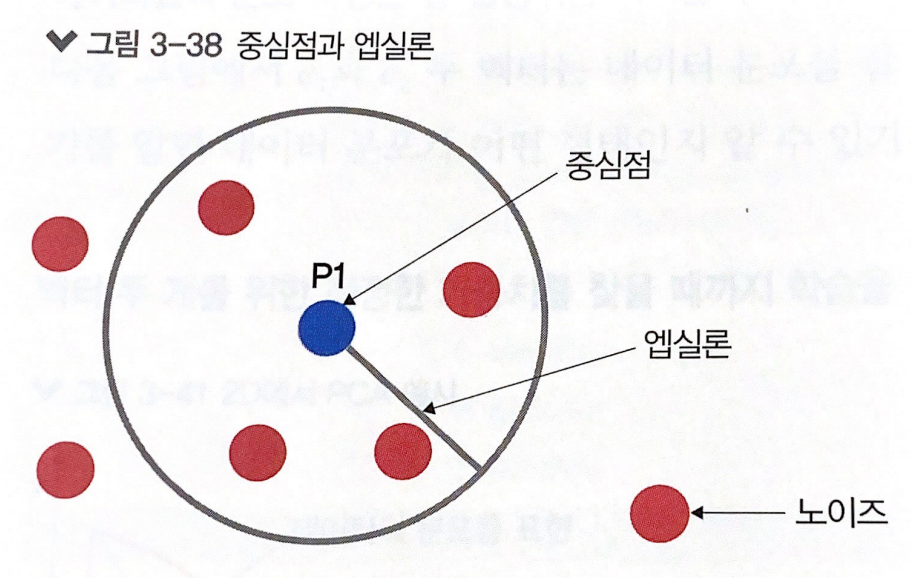
예) mintPts=3인 경우
점 P1에서 거리 엡실론 내에 점이 m(minPts)개 이상 있으면 하나의 군집으로 인식한다고 하자. 이때 엡실론 내에 점(데이터) m개를 가지고 있는 점 P1이 중심점이 됨
//엡실론 : 두 점 사이의 거리로 임계치(범주) 역할을 수행
//m(minPts) : 중심점을 만드는 구성 요건으로 엡실론 내 데이터 개수
2단계. 군집 확장
1단계에서 새로운 군집을 생성했고, 주어진 데이터를 사용해 두 번째 군집을 생성한 후, 두 군집을 하나의 군집으로 확대
밀도가 높은 지역에서 중심점을 만족하는 데이터가 있다면, 그 지역을 포함하여 새로운 군집을 생성

예) P1 왼쪽의 빨간점(초록색 점)을 중심점 P2로 설정
→ minPts=3을 만족
→ 새로운 군집을 생성!

군집 두 개를 하나의 군집으로 확대
3단계. 1~2단계 반복
데이터가 밀집된 밀도가 높은 지역에서 더 이상 중심점을 정의할 수 없을 때까지 1~2단계를 반복
4단계. 노이즈 정의
어떤 군집에도 포함되지 않은 데이터를 노이즈로 정의